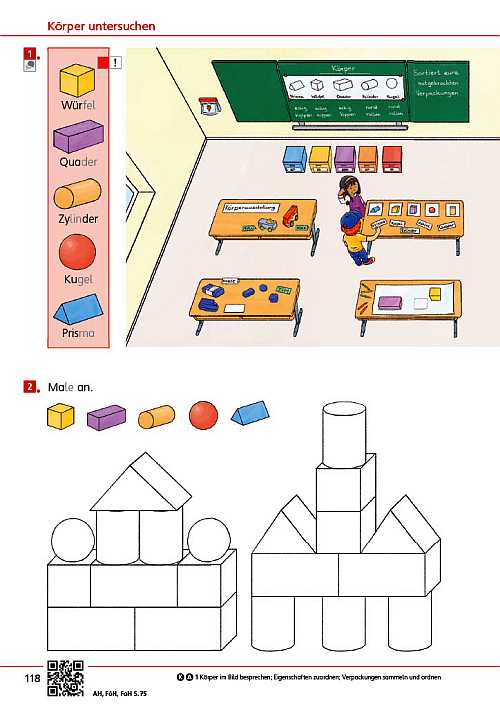
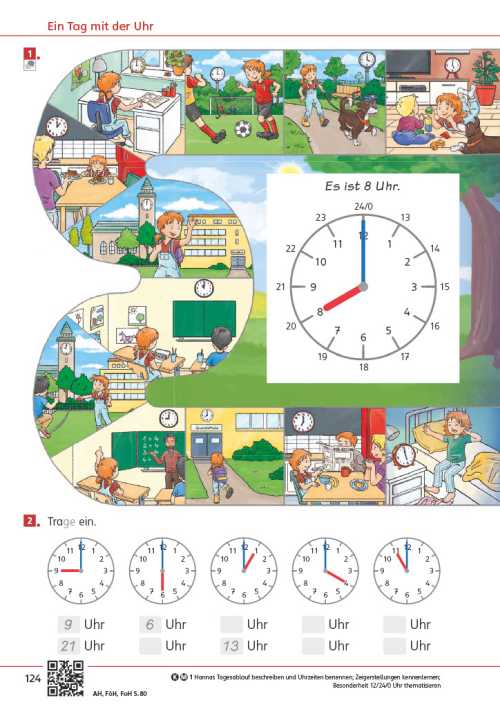
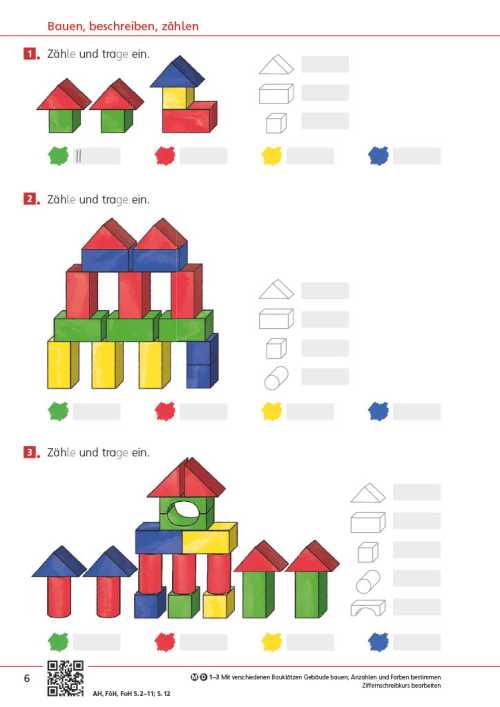
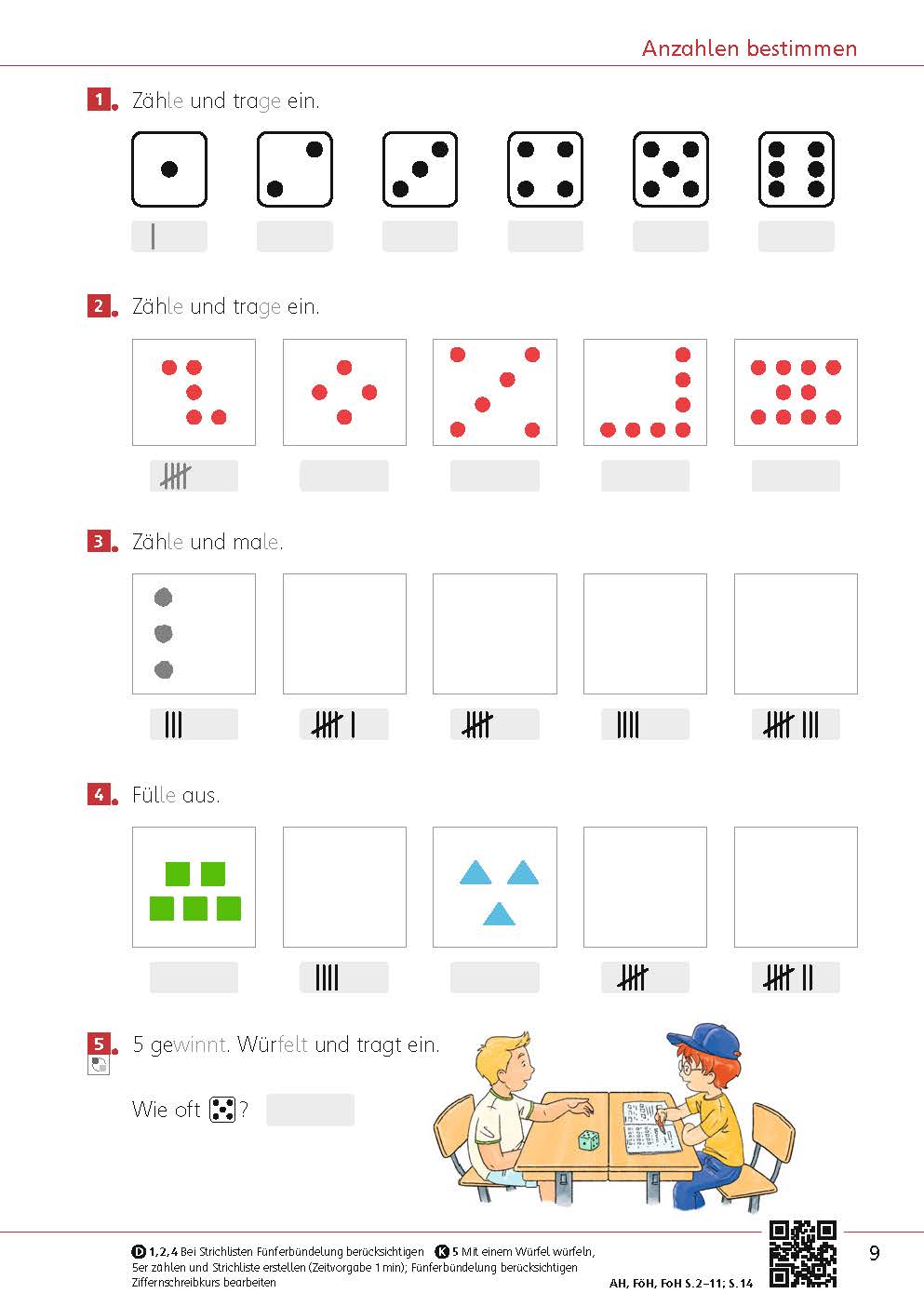
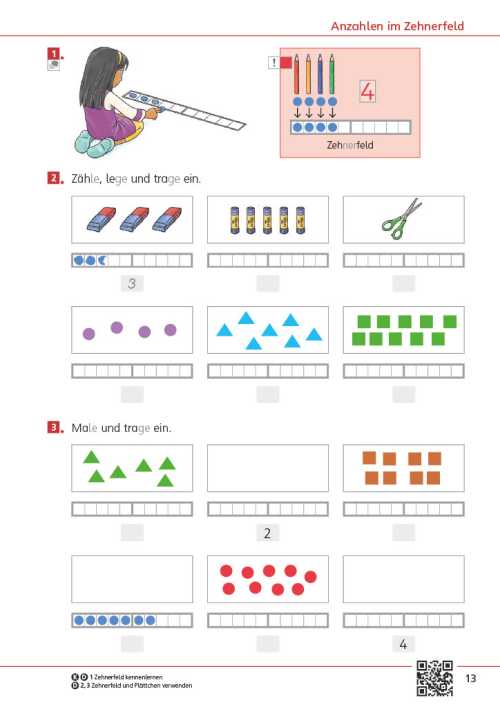
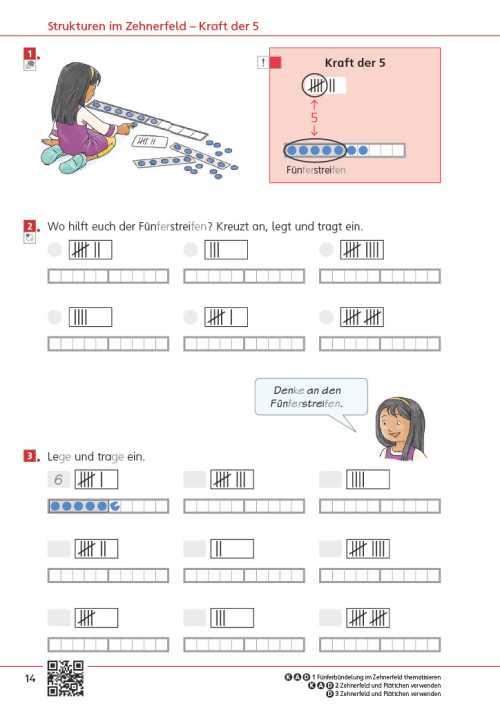
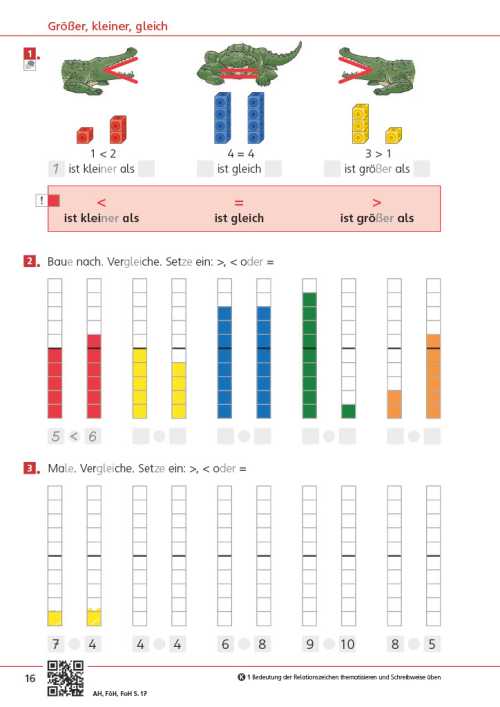
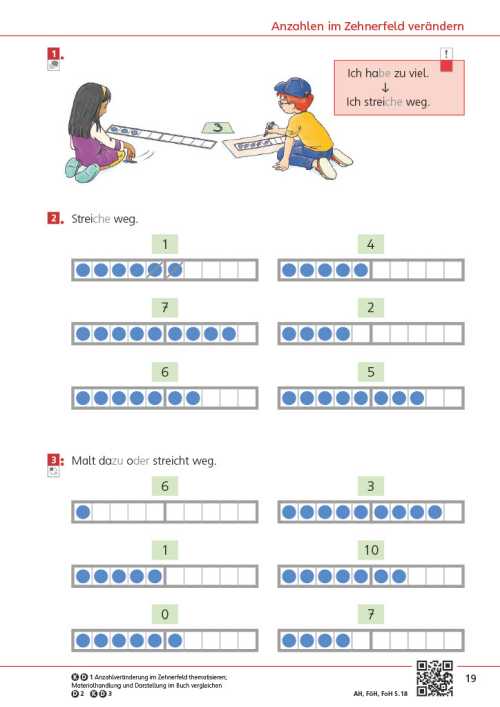
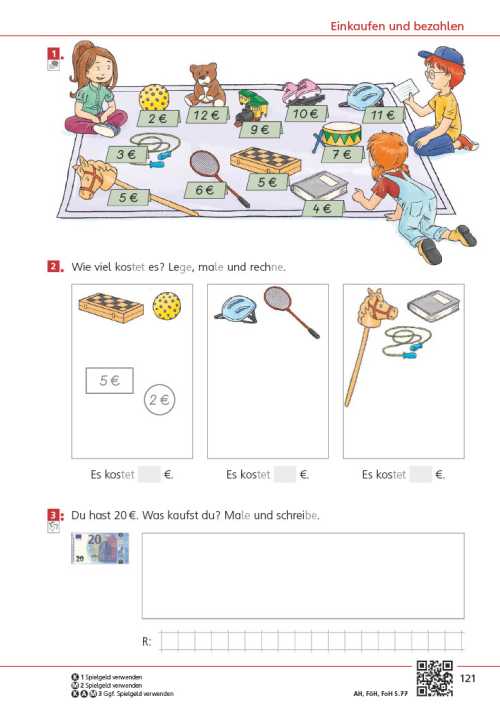
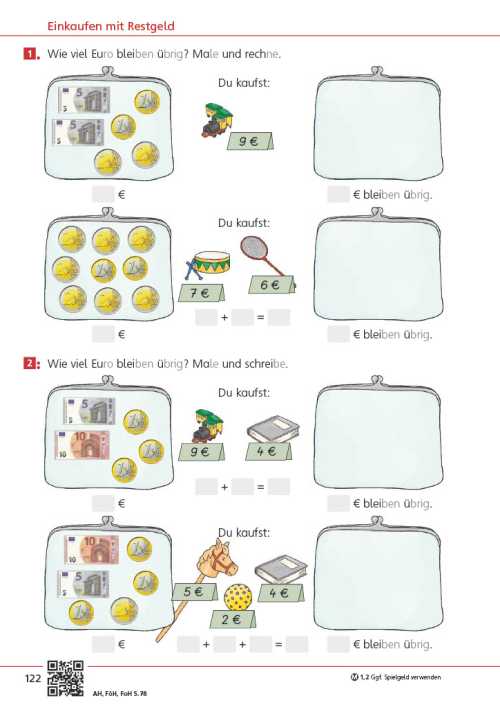
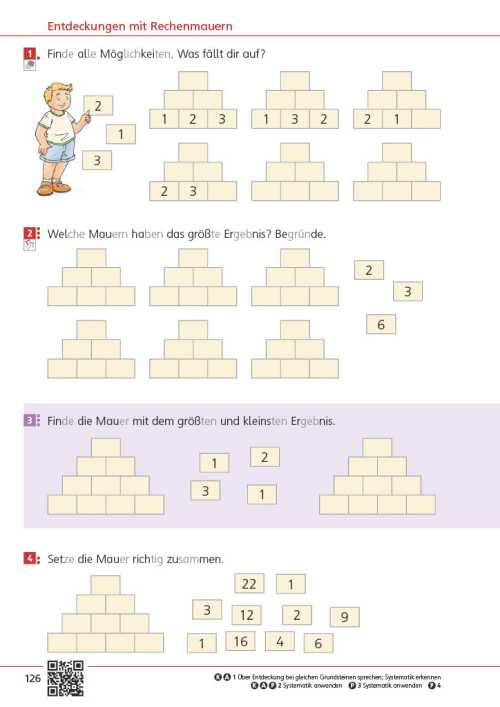
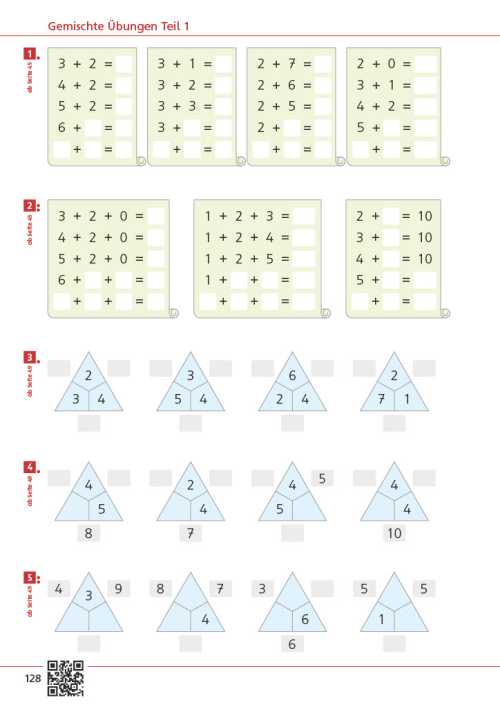
Die Seite bietet einen Einstieg in die Welt der Mathematik. Unterschiedliche Zahldarstellungen und mathematische Handlungen laden dazu ein, sich mit der Welt der Zahlen zu beschäftigen, wobei die unterschiedlichen Zahlaspekte herausgearbeitet werden. Im Fokus steht zunächst das richtige Zählen.
Grundsätzlich unterscheidet man beim Zählen vier Niveaustufen:
- Zahlwortreihe: Die Kinder sagen die Zahlwortreihe auf. Charakteristisch hierfür ist, dass keine einzelnen Zahlwörter zu hören sind, sondern sie es eher zusammenhängen wie eine Reihe bzw. ein „Schlangenwort“ aufsagen („einszweidreivier…“).
- Einzelne Zahlwörter: Was in Schritt eins noch gefehlt hat, findet in Niveaustufe zwei jetzt Beachtung: Die Wörter werden einzeln und hörbar getrennt voneinander ausgesprochen („eins, zwei, drei, vier, …“).
- Beliebiger Anfangspunkt und Rückwärtszählen: Wie der Name schon sagt, können die Kinder auf dieser Niveaustufe einen beliebigen Anfangspunkt wählen, von dem aus sie weiterzählen („sieben, acht, neun, zehn, …“) sowie Rückwärtszählen („neun, acht, sieben, sechs, …“).
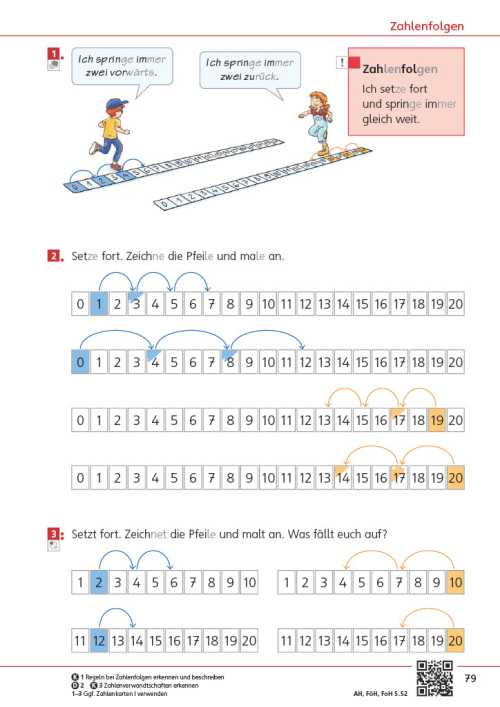
- Zählen in bestimmten Schritten: Das Entdecken und Verstehen von Zahlenfolgen ist hier vor allem relevant („zwei, vier, sechs, acht, …“).
- Flexibles Zählen: Die letzte Stufe enthält keine Einschränkungen mehr – die Kinder können flexibel zählen.
Für Kinder ist es unglaublich wichtig, im Laufe der Zeit die fünfte Niveaustufe zu erreichen. Oft wird die Bedeutung des Zählens unterschätzt. Leider ist es aber häufig der Fall, dass die Kinder die Zahlwortreihe bis 20 einfach auswendig gelernt haben, weshalb man fälschlicherweise davon ausgeht, dass sie bereits ein Verständnis für die Zahlwortbildung entwickelt haben. Dass dies nicht der Fall ist, wird daran ersichtlich, dass die Kinder Fehler im mittleren Zahlenbereich (zwischen 20 und 70) machen.
Im Rahmen der Einführungsseiten werden vor allem die ersten beiden Niveaustufe trainiert und damit der Übergang zum Zählen unter der Verwendung einzelner Zahlwörter fokussiert.
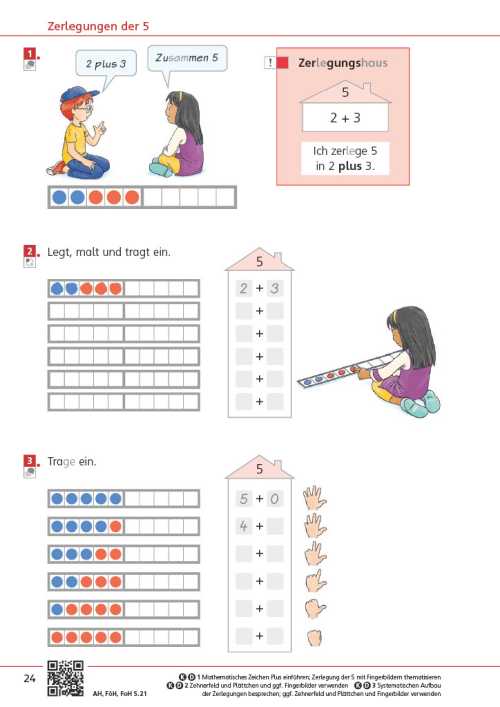
Bei der interaktiven Übung wird das Zahlzeichen mit dem passenden Fingerbild verknüpft wahrgenommen. Die Kinder sollen dann die passende Anzahl an Herzen auf die Tafel ziehen, was wiederum das den Kardinalzahlaspekt trainiert. Die Kinder sehen also ihre ausgewählte Zahl zum einen als abstraktes Zahlzeichen und zum anderen als ihnen vertrautes Fingerbild sowie als Menge in Form von Herzen.