Neben Arithmetik, Geometrie und Stochastik gehört auch sachbezogene Mathematik zu den Kernbereichen der Mathematik, welches als durchgehendes Prinzip fugiert und diese Bereiche miteinander und mit anderen Unterrichtsfächern verbindet. Zudem entstehen durch Sachaufgaben unzählige Anknüpfungspunkte für die Förderung der allgemeinen mathematischen Kompetenzen, was ebenfalls zur Erschließung der Lebenswirklichkeit beiträgt.
Das Mathebuch 2 – Neubearbeitung enthält einen „Methodenkurs – Sachrechnen“ (vgl. Das Mathebuch 2 Neubearbeitung – Handbuch S. 91 – 96). Dieser basiert auf dem idealtypischen Kreislauf nach Blum und Leiß (2005), welcher beschreibt, wie mathematikhaltige Informationen aus Sachsituationen und -kontexten prototypisch entnommen werden. Natürlich laufen die tatsächlichen Modellierungsprozesse nicht so linear ab. Dennoch kann hieraus ein schrittweises Vorgehen abgeleitet werden, worauf folgende Module des Methodenkurses fußen:
- Fragen (Seite 16)
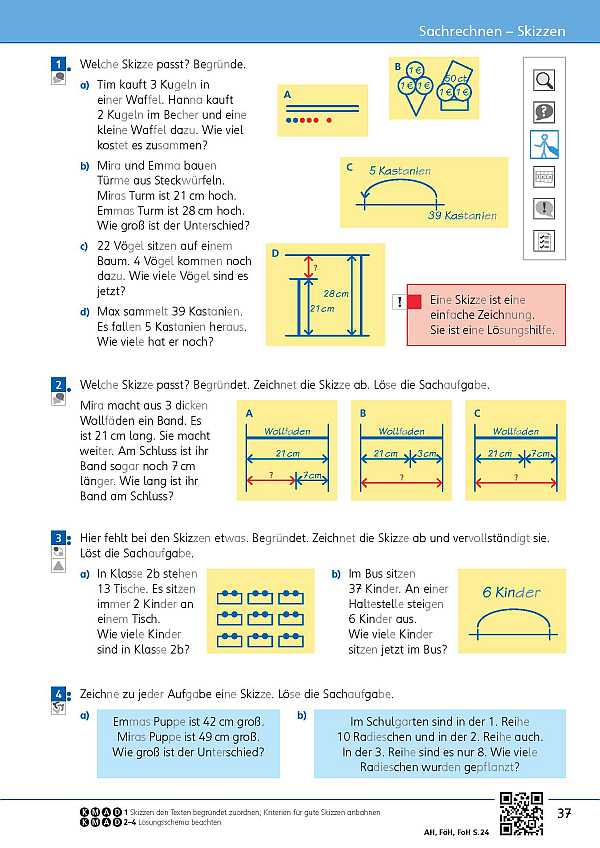
- Skizzen (Seite 37)
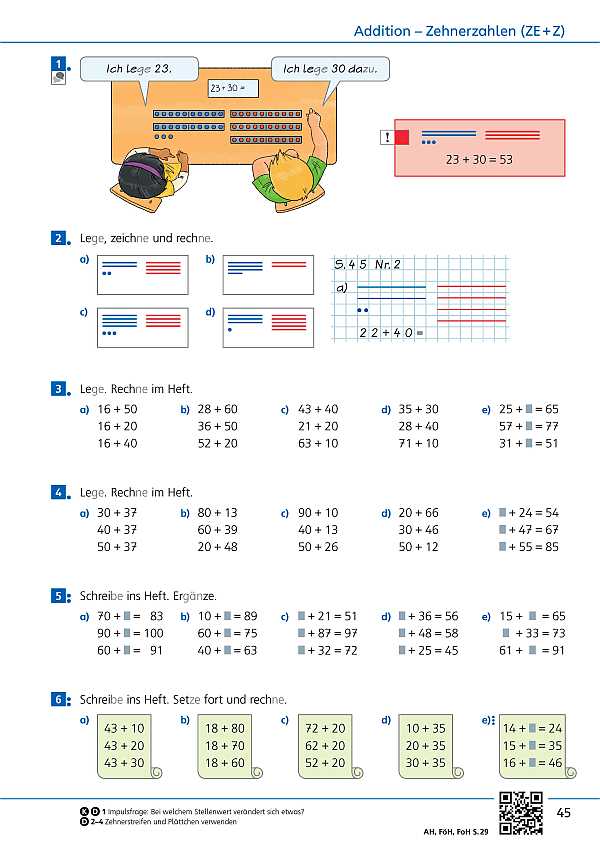
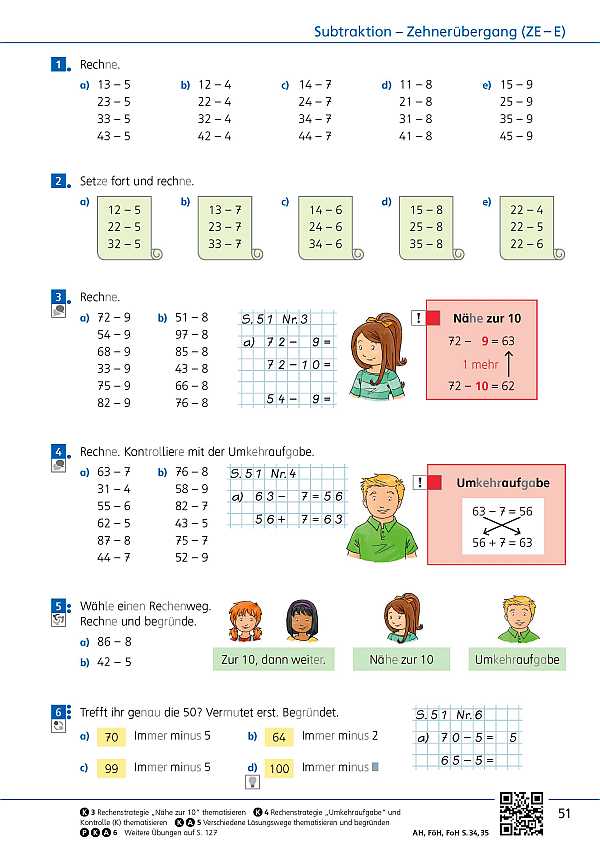
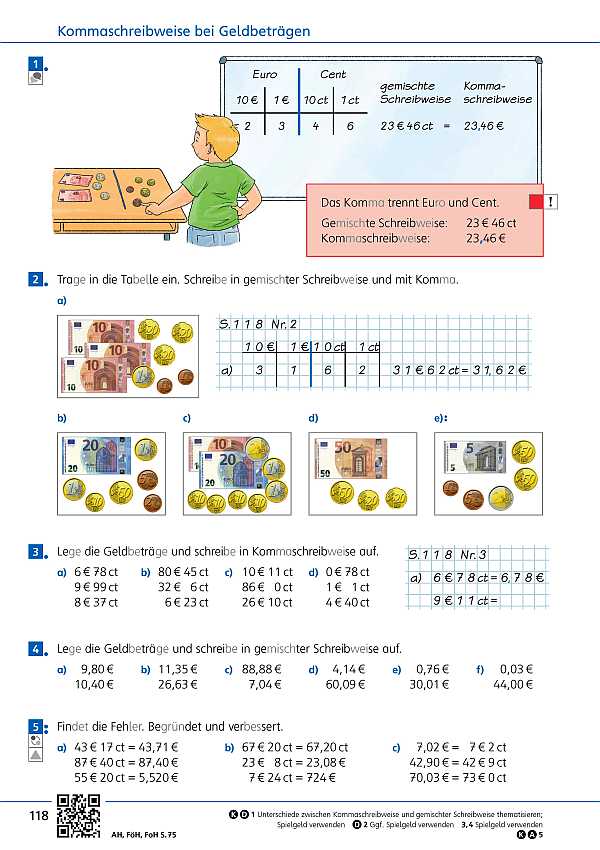
- Rechnungen (Seite 52)
- Antworten (Seite 62) und Übungen (Seite 63)
- Antworten prüfen (Seite 91)
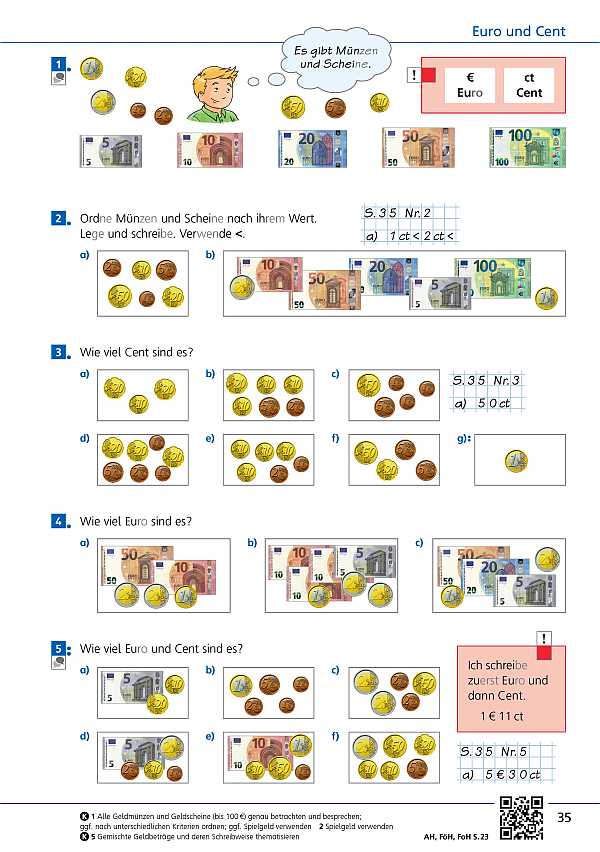
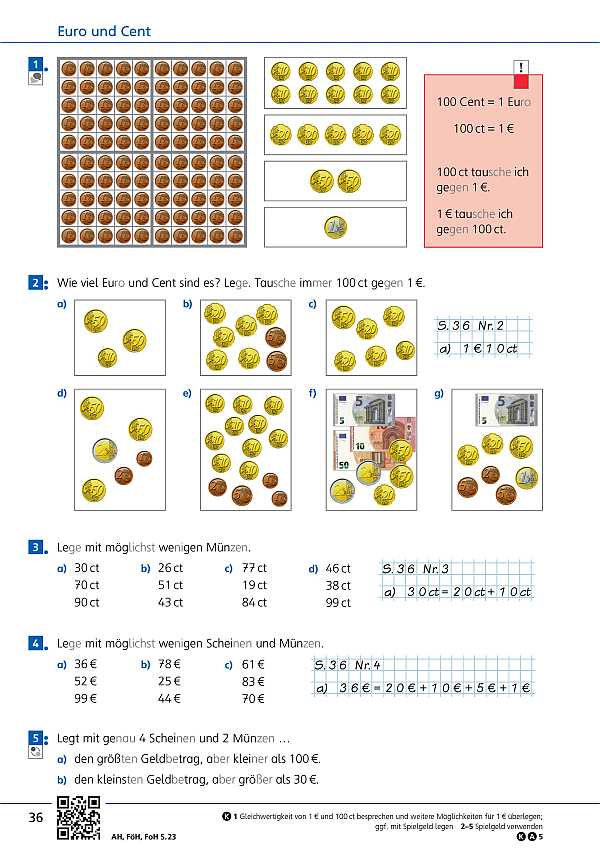
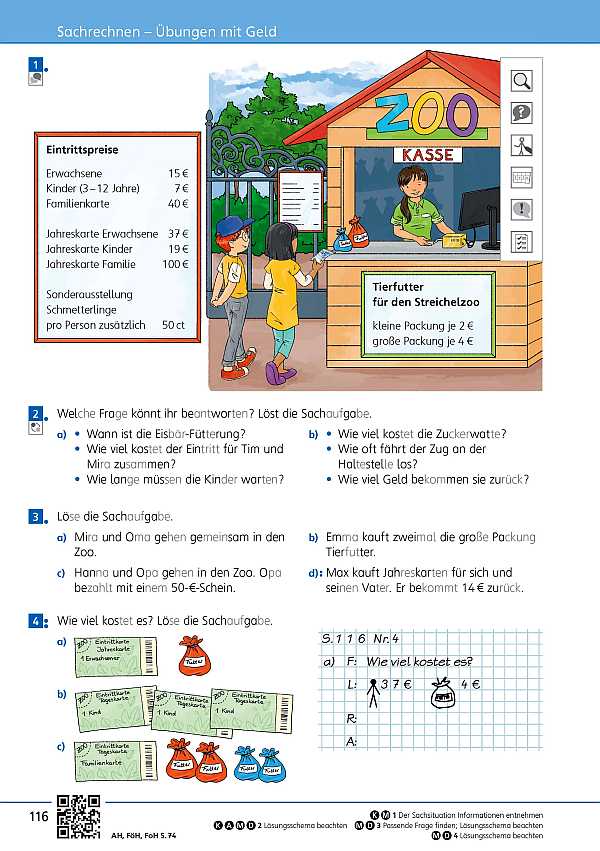
- Übungen mit Geld (Seite 116 / Seite 117)
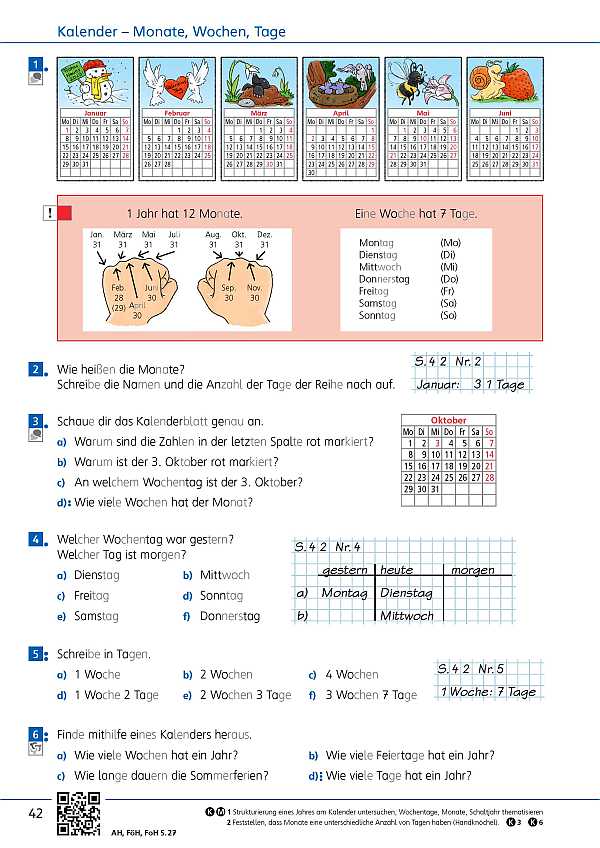
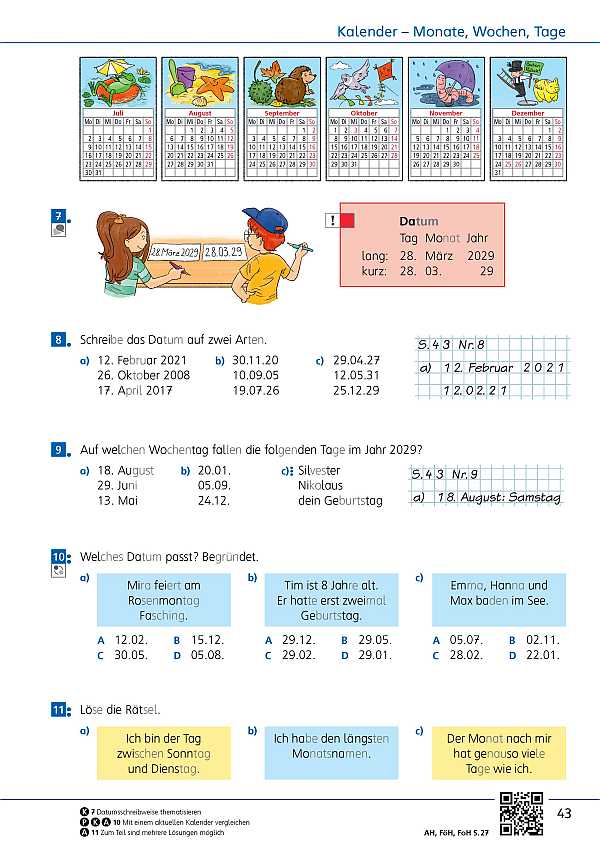
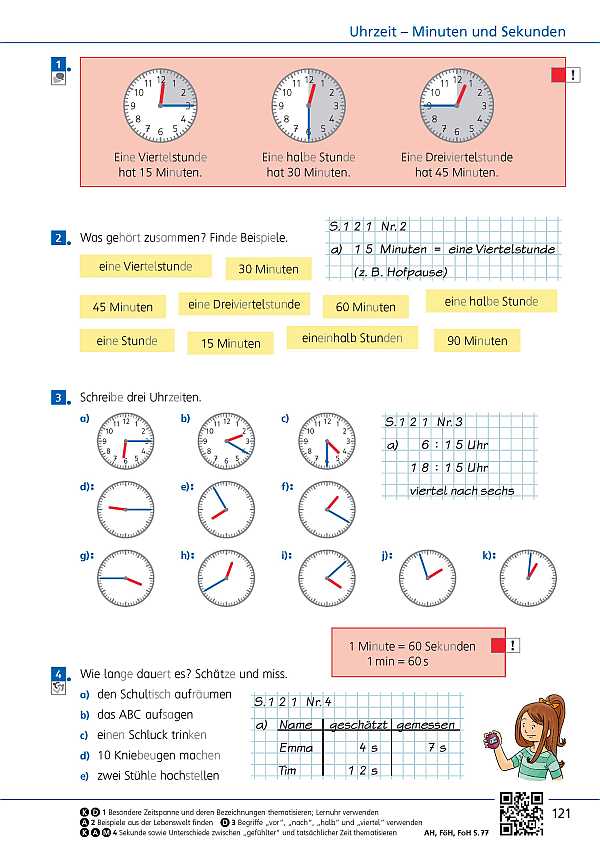
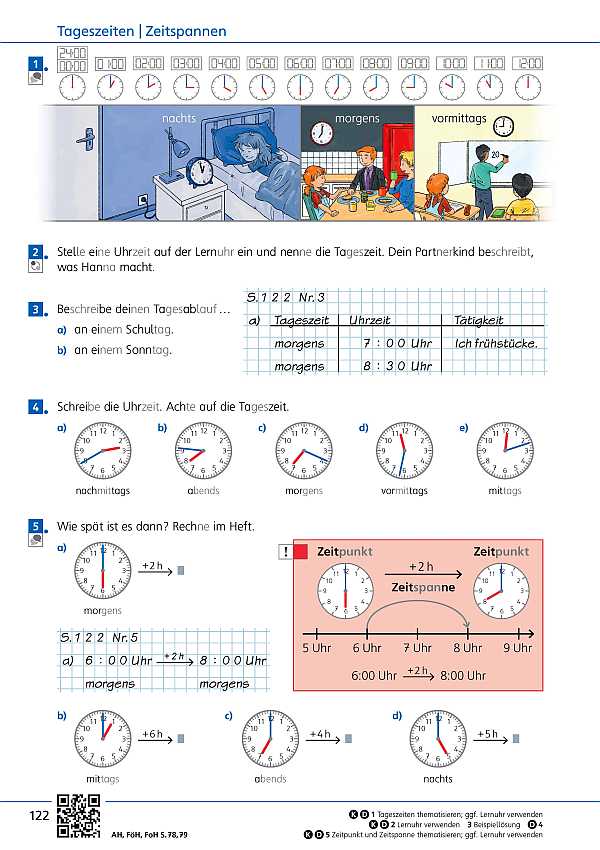
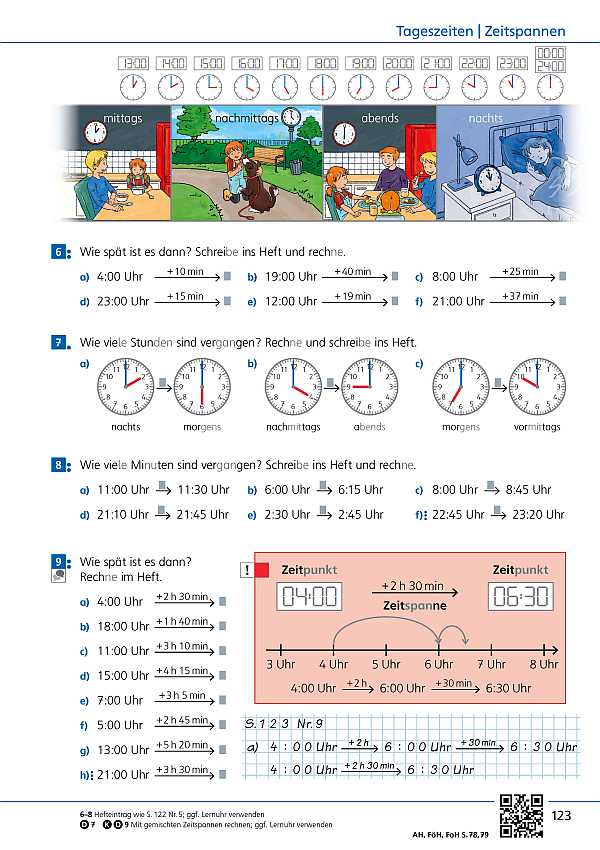
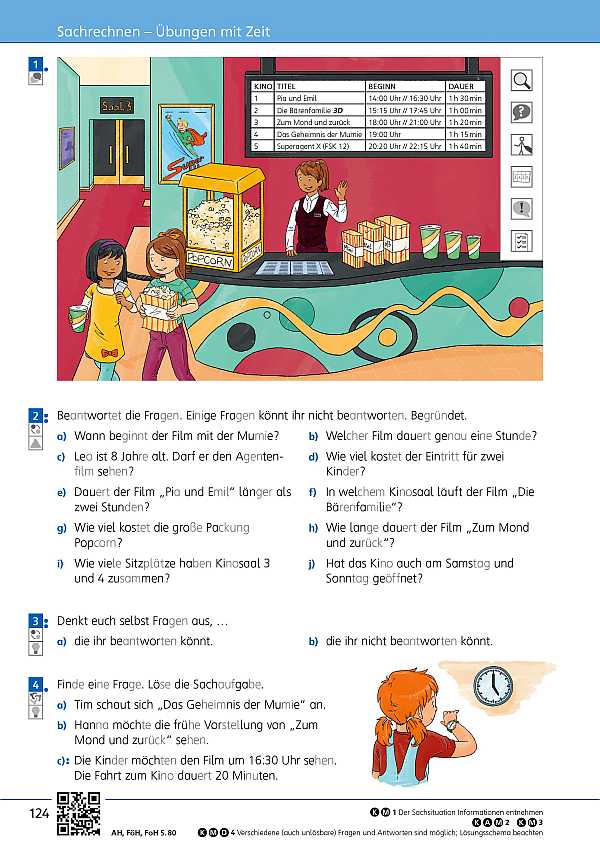
- Übungen mit Zeit (Seite 124 / Seite 125)
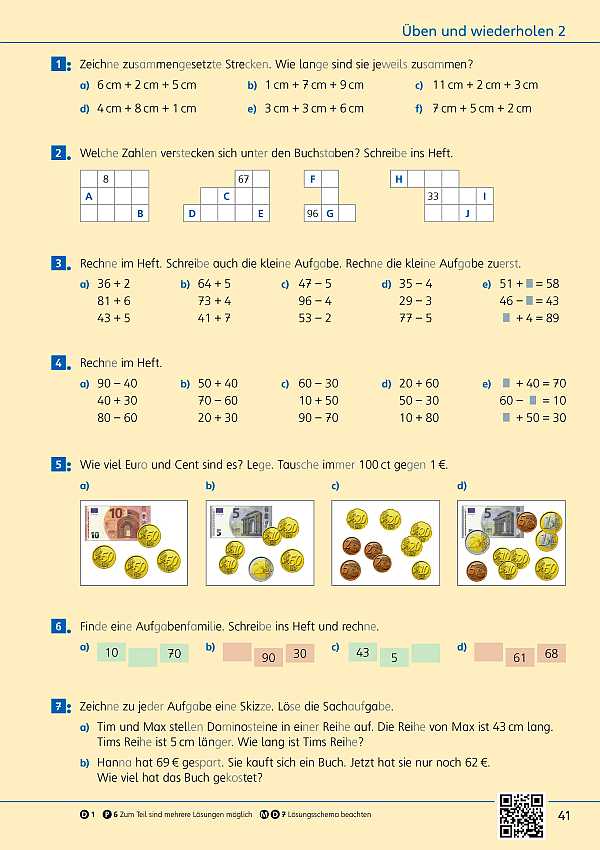
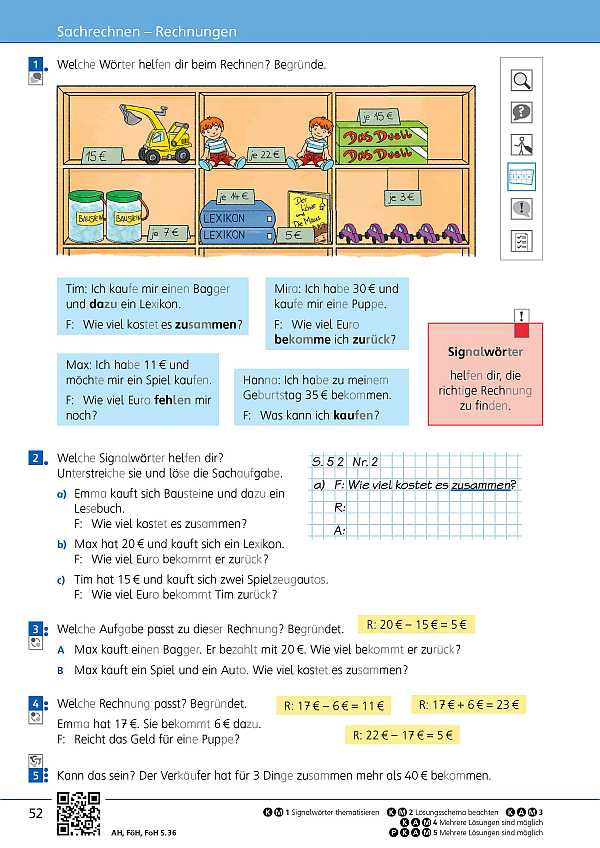
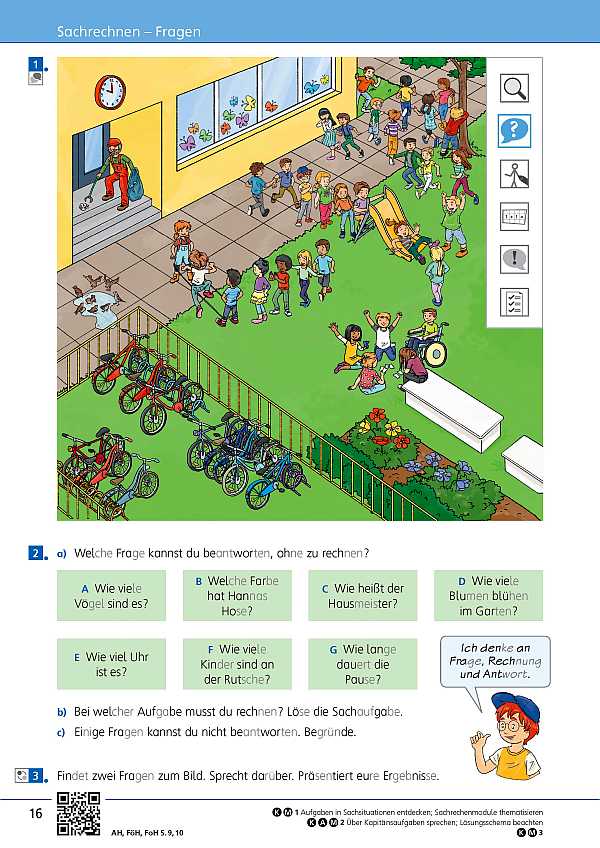
Diese Seite beinhaltet den ersten Methodenkurs: „Fragen“. Die Kinder vertiefen den Zusammenhang zwischen Sachsituation und Fragestellung. Dabei trainieren sie die Unterscheidung zwischen Informations- und Rechenfragen. Die Kinder wenden das Lösungsschema „Frage – Rechnung – Antwort“ an. Ziel ist es, dass sie Fragen stellen, untersuchen sowie relevante Informationen ermitteln.
Mithilfe der interaktiven Übung trainieren die Kinder die Zuordnung von der richtigen Rechenfrage zu einer Sachsituation. Diese wird mithilfe eines Bildes dargestellt, woraus die Kinder dann die Frage erkennen sollen, mit welcher eine Sachaufgabe gelöst werden kann.

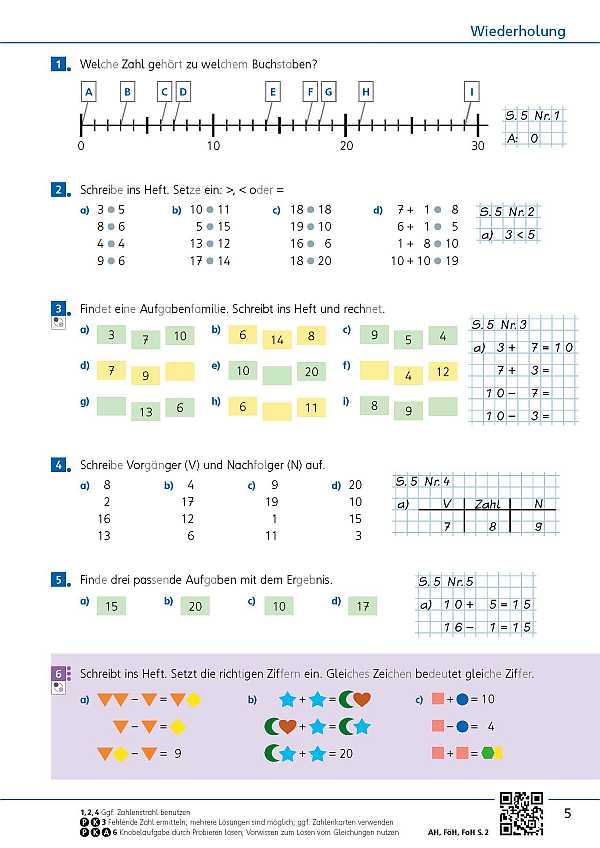


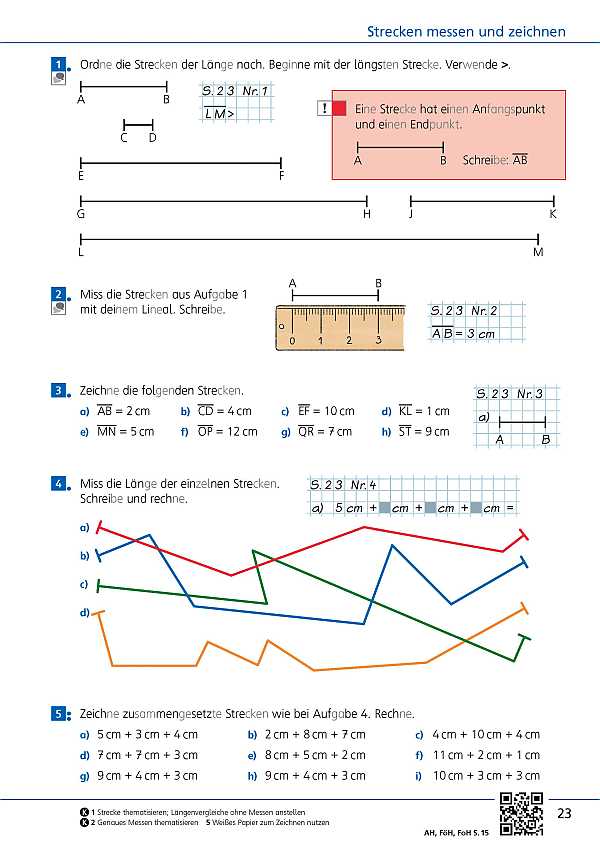
 für Strecke „AB“ thematisiert sowie das Messen und Zeichnen von Strecken.
für Strecke „AB“ thematisiert sowie das Messen und Zeichnen von Strecken.