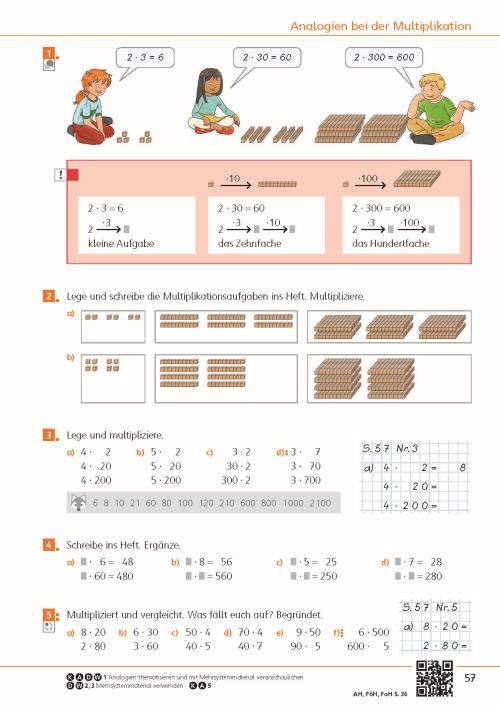
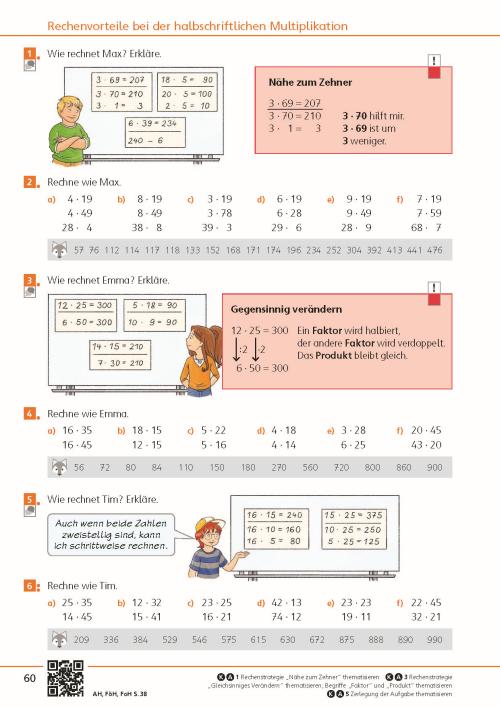
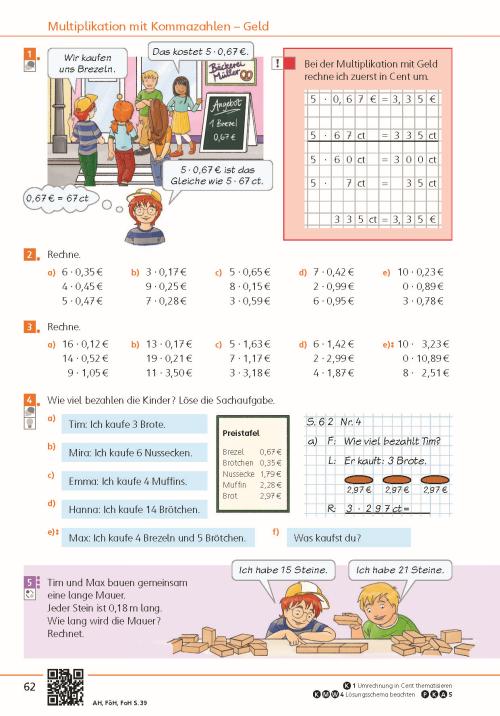
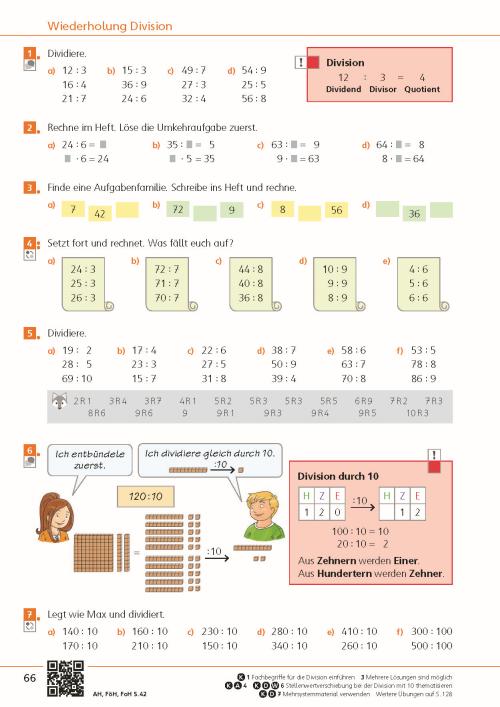
Mathe im Netz
Nach Themen sortieren – Kompetenzen einsehen – Materialeinsatz überblicken... mehr lesen
Unser digitales Angebot für „Mathematik Klasse 3 – Neubearbeitung“ umfasst 106 Elemente. Mithilfe dieser Tabelle können sie alle Inhalte nach Kategorien (Arithmetik, Geometrie, Stochastik etc.), Kompetenzen (Inhaltsbezogene und prozessbezogene Kompetenzen etc.), Materialien (Zehnerfeld, Steckwürfel, Spielgeld etc.), Buchkapiteln und Typen (Lernvideo, interaktive Übung etc.) filtern. So erkennen Sie auf einen Blick, welche Angebote Ihnen zu den jeweiligen Themen zur Verfügung stehen. Genauere Informationen zu den jeweiligen Elementen werden Ihnen mit nur einem Klick auf das entsprechende Feld angezeigt.